This blog post is a sequel of the blog posts 1 and 2.

Special relativity is very simple and elegant theory of symmetry (ignore the last word if you are not familiar with it). Sometimes, a naive thinking may lead to the contradictions in the relativistic physics. For instance consider a tunnel and a train of same proper length with some constant relative velocity between them. There is an observer sitting outside the tunnel (observer A) and one sitting in the train (observer B). Now observer A will see the length of the train little shorter than the tunnel and observer B will see the length of tunnel little shorter than train (relativistic length contraction). Let the tunnel be a special one having two doors at the front (from which the train enters the tunnel) and at the end, capable of shutting down simultaneously. Observer A controls the doors. Now since the length of the train is smaller then that of tunnel according to A, she decides to shut down both the doors at that point of time when she sees the train completely inside the tunnel. On the other hand, the observer sitting in the train will deny the fact that the train can be captured by the tunnel as the train is longer than the tunnel according to her. But relativity says that the physics is invariant in any inertial frame therefore both the observers must concur on the facts (whether the train passes or gets captured).

The paradox is resolved by the fact that the shutting of doors is simultaneous in the coordinate chart of observer A and not in the frame of observer B (we have seen in previous blog post, the notion of simultaneity is frame dependent). The observer B sees the door at the end shutting first, which stops the train instantaneously (infinite acceleration), and then the door at front closing. Therefore both the observers will report the same fact, that is, the tunnel captures the train. Here we emphasize again, the events may not be mapped to same coordinates in different coordinate charts. To map the coordinates, of an event, form one inertial coordinate system to another, we must use Lorentz transformation.

Another common paradox that arises is as follows. Consider two twins Alice and Bob living in an inertial coordinate system at same location. Alice starts traveling in a spaceship, moving with a constant relative speed, say meters per light second with respect to Bob along x-axis, for some time (in the frame of the observer B) and then comes back to Bob with same the relative velocity. Now, naively, one can say that according to Bob, the time of Alice goes slower than him, hence when Alice returns, he must age more. According to Alice, Bob’s time goes slowly (moving clocks are slower for Alice too!) and therefore Alice should age more when she returns. But both Alice and Bob should agree on the same fact and here lies the paradox which everyone comes by when studying the relativity for the first time.

We will attack this problem from the perspective of the naive thinking which is based on the assumption that the physical phenomenon is symmetric from the point of view of Alice and Bob. So first let us think how many coordinate charts we require to study the problem?

No, not two but three. In first coordinate chart (of observer B) Bob is at rest at some position (from where Alice starts her journey). In second coordinate chart (of observer A), Alice is at rest at some position when going away from Bob and in third coordinate chart (of observer A’), Alice is at rest at some position when returning back towards Bob. Also note that Alice and Bob are not observers according to our definition in the blog post. So it is Alice who “jumps” from one coordinate chart to another whereas Bob remains in the same frame of reference. Thus the physical phenomenon is not symmetric from the point of view of Alice and Bob.

The word “jumps” has been used because we assume that she accelerated infinitely when changing her direction. Now the postulates of special relativity being valid for the inertial frames doesn’t mean that we can’t study accelerated objects. We can perfectly study the accelerated objects by using the notion of comoving frames. In our example, second and third frames are the comoving frames for Alice. Similarly one can study finitely accelerating objects by considering a series of jumps (of the system) from one comoving frame to another.

The the Minkowski graph of the observer B is (tracking of the coordinate is not necessary). Different colors represent the time coordinate axis of different frames.In this graph, the green line is the world line of Bob and the world line of Alice is represented by the violet line and red line. One can clearly see that Bob ages by 30 light seconds and Alice ages by 24 light seconds.

Now let us look at the graph of the observer A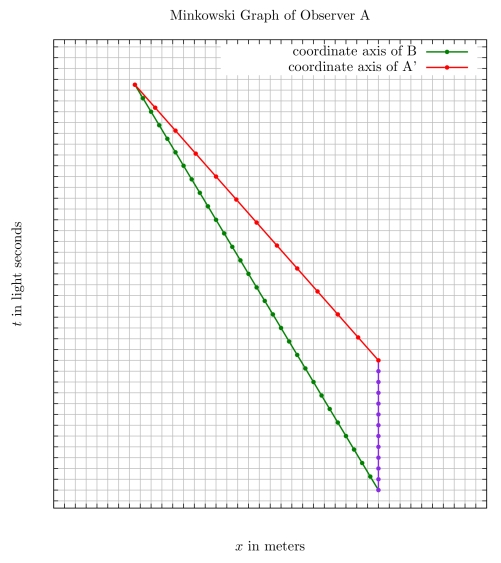
Here one can observe that in the coordinate chart of observer A, Alice ages faster than Bob for half of her trip. For the next half, she ages much slower then Bob (who ages 30 light seconds) such the in the end of the journey, Alice ages less (again 24 light seconds) than Bob.

And finally we see the graph of the observer A’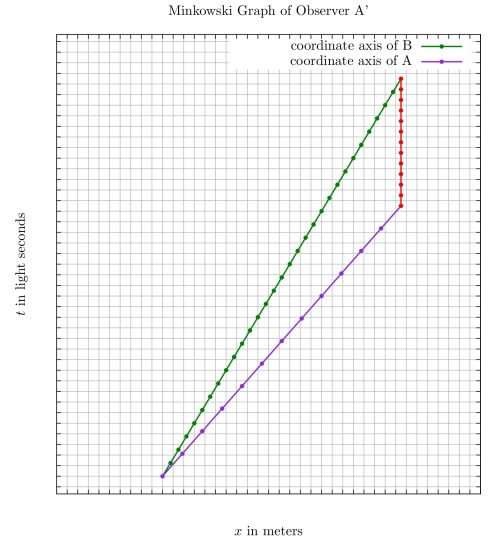

From these three graphs we see that all the observers (A, A’ and B) agree that Bob has aged more than Alice in this trip, by 6 light seconds. It means all the inertial observers observed the same physical phenomenon, as required by the first postulate of special relativity, thus resolving the twin paradox.